ৰৈখিক সমীকৰণৰ যুগল (Pair of Linear Equations)
ৰৈখিক সমীকৰণৰ পৰিচয়
ৰৈখিক সমীকৰণ (Linear Equation) হৈছে সেই ধৰণৰ সমীকৰণ য’ত চলকবোৰৰ ঘাত সদায় ১ হয় আৰু কোনো চলকৰ গুণফল ৰৈখিক ৰূপত থাকে। উদাহৰণস্বৰূপে, x + y = 5। যদি আমাৰ দুটা চলক x আৰু y থাকে আৰু দুটা ৰৈখিক সমীকৰণ থাকে, তেতিয়া সেই সমীকৰণ যুগলক “Pair of Linear Equations” বোলা হয়। এই যুগলৰ সমাধান মানে সেই চলকবোৰৰ মান পোৱা য’ত দুয়োটা সমীকৰণ সন্তুষ্ট হয়। ৰৈখিক সমীকৰণৰ যুগল শিক্ষাৰ অন্যতম মুখ্য বিষয়, বিশেষকৈ **Class 10** গণিতৰ বাবে।
উদাহৰণ:
2x + 3y = 7
x – y = 1
এই যুগলৰ সমাধান মানে সেই (x, y) য’ত দুয়োটা সমীকৰণে সত্য হয়। ৰৈখিক সমীকৰণৰ যুগলৰ সমাধান তিনিটা ধৰণৰ হ’ব পাৰে:
- একক সমাধান (Unique solution) – একে এক মাত্ৰা বিন্দু
- অসীম সমাধান (Infinite solutions) – দুয়োটা সমীকৰণ একে লাইনে থাকে
- সমাধান নাই (No solution) – ৰেখাবোৰ পাৰস্পৰিক ছেদ নকৰে
ৰৈখিক সমীকৰণৰ যুগলৰ মানক ৰূপ
দুটা ৰৈখিক সমীকৰণ সাধাৰণতে এই ৰূপত থাকে:
ax + by = c
dx + ey = f
য’ত, a, b, c, d, e, f হ’ল ধ্ৰুৱ সংখ্যা আৰু x, y হ’ল চলক।
এই মানক ৰূপ ব্যৱহাৰ কৰি সমাধানৰ পদ্ধতি সহজে বুজা যায়।
উদাহৰণ: 3x + 2y = 10
x – y = 1
ৰৈখিক সমীকৰণ যুগলৰ সমাধানৰ আগতে, প্ৰথমে চাওঁক যে সমীকৰণবোৰ সমান্তৰাল নে নাই।
যদি a/d = b/e ≠ c/f → সমাধান নাই (No solution)
যদি a/d = b/e = c/f → অসীম সমাধান (Infinite solutions)
অন্যথা → একক সমাধান (Unique solution)
সমাধানৰ পদ্ধতি
ৰৈখিক সমীকৰণৰ যুগল সমাধানৰ প্ৰধান পদ্ধতি:
- প্ৰতিস্থাপন পদ্ধতি (Substitution Method) – এক সমীকৰণৰ পৰা এক চলক সমাধান কৰি দ্বিতীয়ত প্ৰতিস্থাপন কৰা।
- সমন্বয় পদ্ধতি (Elimination Method) – চলকবোৰ ক্ৰমান্বয়ে বাদ দি এক সমীকৰণত পৰিণত কৰা।
- গ্ৰাফিক পদ্ধতি (Graphical Method) – প্ৰতিটো সমীকৰণৰ রেখা আঁকি পৰস্পৰৰ ছেদ বিন্দু পোৱা।
- মেট্ৰিক্স আৰু ডিটাৰমিনেণ্ট পদ্ধতি (Matrix/Determinant Method) – প্ৰি-উচ্চতৰ গণিতত ব্যৱহাৰ কৰা হয়।
প্ৰত্যেক পদ্ধতিত ধাপে ধাপে কৰা সমাধান সহজে বুজা যায় আৰু বিভিন্ন সমস্যাৰ বাবে ব্যৱহৃত হয়। Class 10 ৰ বাবে সাধাৰণতে প্ৰথম তিনিটা পদ্ধতি যথেষ্ট।
উদাহৰণ আৰু ব্যাখ্যা
উদাহৰণ 1: সমীকৰণ যুগল
x + y = 4
x – y = 2
Step 1: দ্বিতীয় সমীকৰণৰ পৰা x = y + 2
Step 2: প্ৰথম সমীকৰণত প্ৰতিস্থাপন কৰক: (y + 2) + y = 4 → 2y + 2 = 4 → y = 1
Step 3: x = y + 2 → x = 3
সেয়ে সমাধান: (x, y) = (3, 1)
উদাহৰণ 2: সমীকৰণ যুগল
2x + 3y = 7
4x + 6y = 14
যদি সমীকৰণ দুয়োটা একে লাইনে থাকে → অসীম সমাধান
উদাহৰণ 3: সমীকৰণ যুগল
x + 2y = 5
2x + 4y = 12
যদি সমীকৰণ সমান্তৰাল হয় → সমাধান নাই
গ্ৰাফিক প্ৰতিনিধিত্ব
গ্ৰাফৰ জৰিয়তে ৰৈখিক সমীকৰণ যুগলৰ সমাধান বুজা সহজ। উদাহৰণ স্বৰূপ:
সমীকৰণ: x + y = 4
x – y = 2
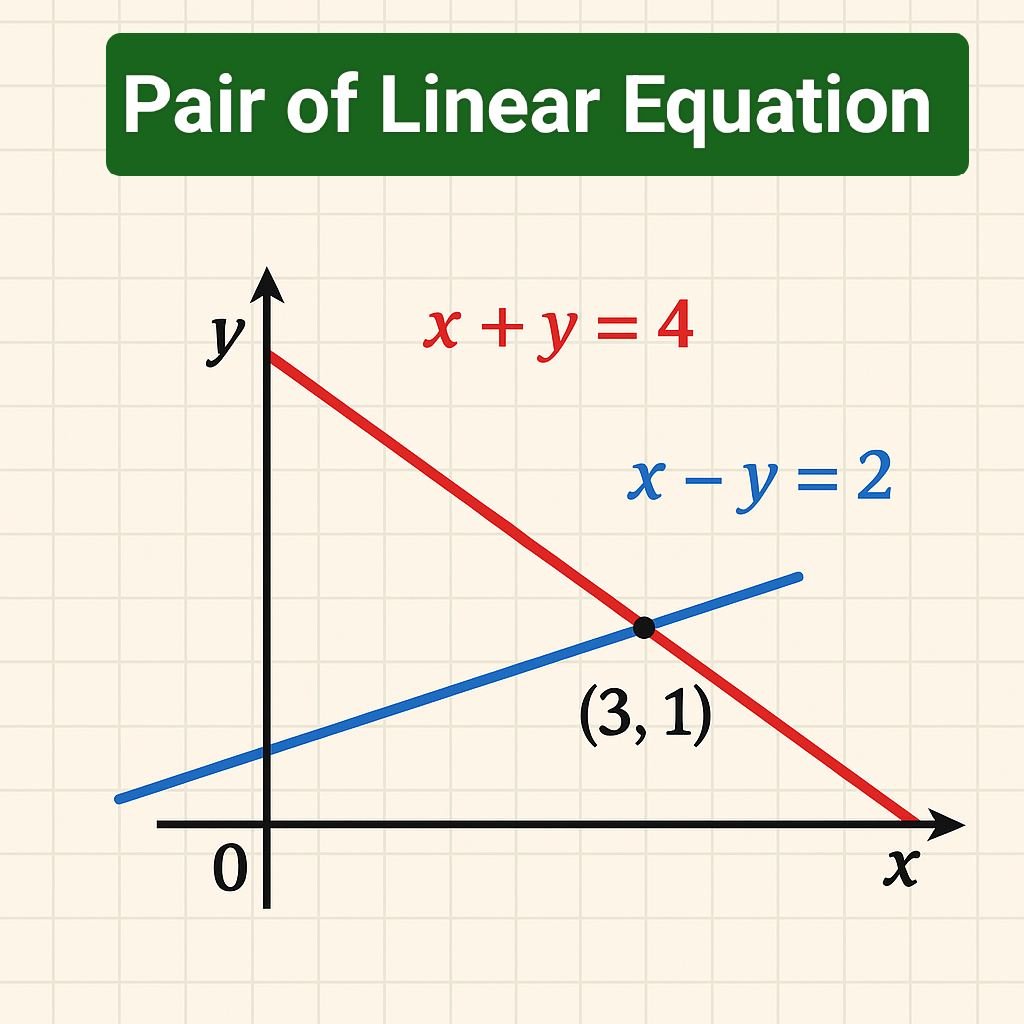
গ্ৰাফত দেখিবলৈ পোৱা যায় যে দুয়োটা রেখাৰ ছেদ বিন্দুত x = 3, y = 1
এই চিত্ৰখনত দুটা ৰৈখিক সমীকৰণ দেখুওৱা হৈছে — x + y = 4 (ৰঙা ৰেখা) আৰু x − y = 2 (নীলা ৰেখা)।
প্ৰতিটো ৰৈখিক সমীকৰণে এটা সোজা ৰেখা প্ৰতিনিধিত্ব কৰে। “ৰৈখিক” মানে হ’ল “সোজা ৰেখা” — ইয়াত x আৰু y ৰ মানবোৰ একেলগে পৰিবৰ্তন কৰিলে একেটা সোজা ৰেখা পোৱা যায়।
ৰঙা ৰেখা (x + y = 4) দেখুৱায় x আৰু y ৰ এনে মানবোৰ যিবোৰ একেলগে যোগ কৰিলে ৪ হয়। উদাহৰণস্বৰূপে, যদি x = 3, তেন্তে y = 1; যদি x = 2, তেন্তে y = 2; এইদৰে ইয়াৰ ওপৰত থকা সকলো বিন্দুৱে এই সমীকৰণটো সন্তুষ্ট কৰে।
নিলা ৰেখা (x − y = 2) দেখুৱায় x আৰু y ৰ এনে মানবোৰ যিবোৰত x ৰ পৰা y বিয়োগ কৰিলে ২ হয়। উদাহৰণস্বৰূপে, যদি x = 3, তেন্তে y = 1; যদি x = 4, তেন্তে y = 2; ইত্যাদি। এইদৰে ইয়াৰ ওপৰত থকা সকলো বিন্দুৱে এই দ্বিতীয় সমীকৰণটো সন্তুষ্ট কৰে।
এতিয়া লক্ষ্য কৰা, এই দুটা ৰেখা একে ঠাইত মিলিছে — যি বিন্দু (3, 1)। এই মিলন বিন্দুটোকেই দুয়োটা ৰেখাৰ “সংযোগ বিন্দু” বোলা হয়। এই ঠাইত দুয়োটা সমীকৰণ একেলগে সত্য হয়।
- প্ৰথম সমীকৰণ: x + y = 4 ⇒ 3 + 1 = 4 ✔️
- দ্বিতীয় সমীকৰণ: x − y = 2 ⇒ 3 − 1 = 2 ✔️
অৰ্থাৎ, x = 3 আৰু y = 1 মান দিলে দুয়োটা সমীকৰণ একেলগে পূৰণ হয়। এই বাবে, (3, 1) হ’ল এই “Pair of Linear Equations” ৰ একেমাত্ৰ সমাধান।
এই ধৰণৰ ৰৈখিক সমীকৰণৰ জোড়াক consistent pair বোলা হয়, কাৰণ ই একেলগে মিলি একেটা বিন্দুত কাটি যায়। যদি দুটা ৰেখা একেলগে নাকাটি, বা একে ৰেখাত পৰে, তেন্তে সমীকৰণবোৰৰ ধৰণ বেলেগ হয় (inconsistent বা infinitely many solutions)।
এই উদাহৰণটো আমাক দেখুৱায় যে, দুটা ৰৈখিক সমীকৰণৰ মিলন বিন্দুই সেই সমীকৰণ জোড়াটোৰ সমাধান। এই কথাটো গণিতৰ ভিতৰত অত্যন্ত গুৰুত্বপূর্ণ, বিশেষকৈ যেতিয়া আমাৰ x আৰু y ৰ সঠিক মান বিচাৰিবলৈ হয়।
প্ৰয়োগ
ৰৈখিক সমীকৰণ যুগলৰ প্ৰয়োগ বিস্তৃত। কিছু উদাহৰণ:
- ব্যৱসায়: লাভ আৰু ক্ষতিৰ হিসাব
- অভিয়ন্ত্ৰণ: সঁজুলি আৰু উপাদান বণ্টন
- অর্থনীতি: খৰচ আৰু আয়ৰ সমীকৰণ
- প্ৰাকৃতিক সমস্যাৰ মডেলিং: গতি, দূৰত্ব, সময়
